¿En qué día de la semana cae una fecha determinada?
¿En qué día de la semana cae una fecha determinada? En lunes, martes, etc... Existen varios algoritmos que se encargan de calcularlas,[Ver ZELLER] pero en Visual Basic .NET la forma de calcularla es directa ya que las estructuras que contiene una fecha (Date) tienen una función [Ver DayOfWeek] que se encarga de realizar ese calculo
''' <summary> ''' Devuelve un numero que representa el día de la semana ''' en la que cae una fecha. ''' Por ejemplo, el día 1 de enero de 2010 fue 5 (Viernes) ''' </summary> ''' <param name="unaFecha">la fecha que se analiza</param> ''' <returns> ''' <para> ''' Uno de los valores de la enumeracion DayOfWeek que indica ''' el día de la semana del objeto DateTimeOffset actual. </para> ''' <para> Un numero (entre 0 y 6) que representa el día de ''' la semana con los siguientes valores</para> ''' <para> 0 = domingo</para> ''' <para> 1 = lunes</para> ''' <para> 2 = martes</para> ''' <para> 3 = miércoles</para> ''' <para> 4 = jueves</para> ''' <para> 5 = viernes</para> ''' <para> 6 = sábado</para> ''' </returns> ''' <remarks> ''' <example> ''' DateTimeOffset.DayOfWeek (Propiedad) ''' <code>http://msdn.microsoft.com/es-es/library/system.datetimeoffset.dayofweek.aspx</code> ''' </example> ''' <example> ''' DayOfWeek (Enumeración) ''' <code>http://msdn.microsoft.com/es-es/library/system.dayofweek.aspx</code> ''' </example> ''' </remarks> Public Shared Function DayOfWeek1( _ ByVal unaFecha As DateTimeOffset) As Integer Return unaFecha.DayOfWeek End Function
También se puede mostrar el nombre del día de la semana de una fecha determinada usando el especificador de formato "D" o el especificador de formato personalizado "dddd". Por ejemplo:
'Manual del programador de .NET Framework 'Cadenas de formato de fecha y hora 'http://msdn.microsoft.com/es-es/library/97x6twsz.aspx 'DateTimeOffset.DayOfWeek(Propiedad) 'http://msdn.microsoft.com/es-es/library/system.datetimeoffset.dayofweek.aspx Dim displayDate As New DateTimeOffset(#1/1/2008 1:18:00 PM#, DateTimeOffset.Now.Offset) Dim provider As System.IFormatProvider = Globalization.CultureInfo.CurrentCulture 'Output: martes, 01 de enero de 2008 Debug.WriteLine(String.Format(provider, "{0:D}", displayDate)) 'Output: 01/01/2008 es mar. Debug.WriteLine(String.Format(provider, "{0:d} es {0:ddd}.", displayDate)) 'Output: 01/01/2008 es martes. Debug.WriteLine(String.Format(provider, "{0:d} es {0:dddd}.", displayDate))
La norma ISO 8601:2004
La norma ISO 8601:2004 en su apartado 3.2.2 define el código de los días de la semana asi como los nombres de los días de la semana ( evidentemente están en ingles) pero lo que interesa resaltar es que la numeración que propone el estándar no coincide con la numeracion que proporciona el algoritmo de Zeller ( y por tanto, la función [DayOfWeek]) la diferencia es la forma de contar, el algoritmo de Zeller proporciona valores del 0 (domingo) 1 lunes… hasta al 6(sábado), mientras que la norma ISO 8601, dice que los valores van desde el 1 lunes al 7 domingo
El siguiente código realiza la transformación de valores
''' <summary> ''' Numero del día de la semana según la norma ISO8601 ''' domingo=7, lunes=1, martes=2,..., sábado=6 ''' </summary> ''' <returns>Un numero que indica el día de la semana, ''' el lunes tiene el valor 1 y el domingo el valor 7</returns> ''' <remarks> '''<para>PROBLEMA No concuerdan los conceptos</para> '''<para> ''' La enumeración DayOfWeek representa el día de la semana ''' en los calendarios que tienen siete días por semana. ''' El valor de las constantes en esta enumeración varía ''' de DayOfWeek.Sunday a DayOfWeek.Saturday. ''' Si se convierte en un entero, su valor varía de cero ''' (que indica DayOfWeek.Sunday) a seis (que indica DayOfWeek.Saturday). ''' </para> '''<para>Problema</para> '''<para> ''' La norma ISO 8601 indica que los valores son 1 para el lunes, ''' 2 martes, etc. 6 sábado y 7 domingo ''' </para> '''<para> -------------------------------------------- </para> '''<para> Nombre Descripción DayOfWeek ISO8601 </para> '''<para> -------------------------------------------- </para> '''<para> Sunday domingo. 0 7 </para> '''<para> Monday lunes. 1 1 </para> '''<para> Tuesday martes. 2 2 </para> '''<para> Wednesday miércoles. 3 3 </para> '''<para> Thursday jueves. 4 4 </para> '''<para> Friday viernes. 5 5 </para> '''<para> Saturday sábado. 6 6 </para> '''<para> -------------------------------------------- </para> '''<example>DayOfWeek ''' <code> http://msdn.microsoft.com/es-es/library/system.dayofweek.aspx</code> '''</example> '''<example>Norma ISO 8601:2004 ''' <code> http://www.phys.uu.nl/~vgent/calendar/downloads/iso_8601_2004.pdf</code> '''</example> '''</remarks> Public ReadOnly Property ISO8601DiaDeLaSemana( _ ByVal unaFecha As DateTimeOffset) As Integer Get Dim resultado As Integer = unaFecha.DayOfWeek If resultado = 0 Then resultado = 7 End If Return resultado End Get End Property
El algoritmo de Zeller
Por último, si lo que queremos es programar nosotros mismos el algoritmo para calcular el número que representa el día de la semana, tendremos que estudiar e implementar el algoritmo de Zeller.
Referencia Bibliográfica: Texto Obtenido de las siguientes fuentes
- Congruencia de Zeller http://es.wikipedia.org/wiki/Congruencia_de_Zeller
- 2.6. What day of the week was 2 August 1953?http://www.tondering.dk/claus/cal/calendar29.txt
La congruencia de Zeller es un algoritmo que permite obtener, a partir de una fecha, el día de la semana que le corresponde.
Se atribuye su creación a Julius Christian Johannes Zeller, un sacerdote protestante alemán que vivió en el siglo XIX. Zeller observó que existía una dependencia entre las fechas del calendario gregoriano y el día de la semana que les correspondía. A raíz de esa observación, obtuvo (se dice que por tanteo), esta fórmula, en apariencia mágica, que lleva su nombre.
Para el calendario Gregoriano la congruencia de Zeller es
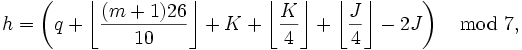
Para el calendario Juliano es:
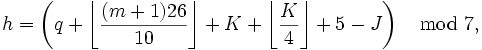
Donde h es el día de la semana (0 = sábado, 1 = domingo, 2 = lunes, …), q es el día del mes, m es el mes, J es la centuria (es realidad ?año / 100?) y K el año de la centuria (año mod 100). Enero y febrero se cuentan como meses 13 y 14 del año anterior.
En las implementaciones informáticas en las que el módulo de un número negativo es negativo, la manera más sencilla de obtener un resultado entre 0 y 6 es reemplazar - 2 J por + 5 J y - J por + 6 J.
Estas fórmulas se basan en la observación de que el día de la semana progresa de una manera predecible basada en cada subparte de esa fecha. Cada término de la fórmula se usa para calcular el desplazamiento necesario para obtener el día correcto de la semana.
Por tanto, para el calendario Gregoriano, las diversas partes de esta fórmula pueden entenderse así:
q representa la progresión del día de la semana basada en el día del mes, dado que cada día sucesivo resulta en un desplazamiento adicional de 1 en el día de la semana.
K representa la progresión del día de la semana basada en el año. Suponiendo que cada año tiene 365 días, la misma fecha de cada año sucesivo será desplazada por un valor de 365 mod 7 = 1
Como hay 366 días en cada año bisiesto, esto de debe tener en cuenta añadiendo un día adicional al valor de desplazamiento del día de la semana. Esto se logra añadiendo [K/4] al desplazamiento. Este término se calcula como un resultado entero. Cualquier resto que pueda haber es descartado. Usando una lógica similar, se puede calcular la progresión del día de la semana para cada centuria observando que hay 36524 días en una centuria normal, y 36525 en cada centuria divisible por 400Dado que 36525 mod 7 =6 y 36524 mod 7 = 5 , el término [J/4]-2J refleja esto (de nuevo usando división entera y descartando cualquier resto fraccional). Para evitar los números negativos, este término se puede reemplazar por 5J+[J/4] con un resultado equivalente
El [ (M+1)26/10]se puede explicar de la siguiente manera. Zeller observó que, al iniciar cada año el 1 de marzo, el día de la semana de cada mes sucesivo progresaba multiplicando el mes por un valor constante y descartando el resto fraccional.
La función globalmod 7�, normaliza el resultado para que se encuentre en el intervalo de 0 a 6, lo que da el índice del día de la semana correcto para la fecha analizada.
La razón por la que la fórmula difiere para el calendario juliano es que este calendario no tiene una regla aparte para las centurias bisiestas y está desplazado con respecto al calendario gregoriano un número fijo de días. Ambas diferencias se pueden tener en cuenta reemplazando el término [J/4]-2J por el término 5 − J, o 5 + 6J para evitar números negativos
Resumiendo:
Si d es el día, m es el mes y y es el año: z:= (700 +(26 * a - 2) DIV 10 + d +b +b DIV 4+ c DIV 4 -2 * c) MOD 7 donde: Si m <=2� (a=m+10 , b=(y-1) MOD 100, c=(y-1) DIV 100 Si m >=3 (a=m-2 , b=y MOD 100 , c=y DIV 100) En la formula anterior z devolverá un valor comprendido entre 0 y 6. Donde 0 es domingo, 1 es lunes y así sucesivamente.
Una forma más fácil del mismo desarrollo es la siguiente
a = (14 - Mes) / 12 y = Año - a m = Mes + 12 * a - 2 Para el calendario Juliano: d = (5 + dia + y + y/4 + (31*m)/12) mod 7 Para el calendario Gregoriano: d = (día + y + y/4 - y/100 + y/400 + (31*m)/12) mod 7 El resultado es un cero (0) para el domingo, 1 para el lunes… 6 para el sábado --------------------------------------------------------------- Ejemplo, ¿En qué día de la semana cae el 2 de agosto de 1953?? ' a = (14 - 8) / 12 = 0 ' y = 1953 - 0 = 1953 ' m = 8 + 12 * 0 - 2 = 6 ' d = (2 + 1953 + 1953 / 4 - 1953 / 100 + 1953 / 400 + (31 * 6) / 12) Mod 7 ' = (2 + 1953 + 488 - 19 + 4 + 15 ) mod 7 ' = 2443 mod 7 ' = 0 ' El valor cero(0) corresponde al domingo.
''' <summary> ''' Devuelve un numero que representa el día de la semana en la que cae una fecha. ''' Por ejemplo, el día 1 de enero de 2010 fue 5 (Viernes) ''' </summary> ''' <param name="año">el año</param> ''' <param name="mes">el mes</param> ''' <param name="dia">el dia</param> ''' <returns>Un numero (entre 0 y 6) que representa el día de ''' la semana con los siguientes valores ''' <para> 0 = domingo</para> ''' <para> 1 = lunes</para> ''' <para> 2 = martes</para> ''' <para> 3 = miércoles</para> ''' <para> 4 = jueves</para> ''' <para> 5 = viernes</para> ''' <para> 6 = sábado</para> ''' </returns> ''' <remarks> ''' <para>Lenguaje: (.NET Framework 3.5) - Visual Basic .NET (Version 9.0) - 2010</para> ''' <example> ''' [wikipedia] Congruencia de Zeller ''' <code>http://es.wikipedia.org/wiki/Congruencia_de_Zeller</code> ''' </example> ''' <autor> Joaquin medina Serrano: joaquin@medina.name</autor> ''' <rights> Licencia Creative Commons Compartir-Igual 3.0</rights> ''' </remarks> Public Shared Function DayOfWeek(ByVal año As Integer, ByVal mes As Integer, ByVal dia As Integer) As Integer ' '--------------------------------------------------------------- ' ATENCION no hay control de datos de entrada ' La fecha que se recibe se supone que es correcta ' No se realiza ninguna comprobación de fechas. '--------------------------------------------------------------- ' '--------------------------------------------------------------- ' Apunte Táctico: Congruencia de Zeller. ' La congruencia de Zeller es un algoritmo que permite obtener, ' a partir de una fecha, el día de la semana que le corresponde '--------------------------------------------------------------- ' a = (14 - Mes) / 12 ' y = Año - a ' m = Mes + 12 * a - 2 ' Para el calendario Juliano: ' d = (5 + dia + y + y / 4 + (31 * m) / 12) Mod 7 ' Para el calendario Gregoriano: ' d = (día + y + y / 4 - y / 100 + y / 400 + (31 * m) / 12) Mod 7 ' El resultado es un cero (0) para el domingo, 1 para el lunes… 6 para el sábado '--------------------------------------------------------------- ' Ejemplo, ¿En qué día de la semana cae el 2 de agosto de 1953?? ' a = (14 - 8) / 12 = 0 ' y = 1953 - 0 = 1953 ' m = 8 + 12 * 0 - 2 = 6 ' d = (2 + 1953 + 1953 / 4 - 1953 / 100 + 1953 / 400 + (31 * 6) / 12) Mod 7 ' = (2 + 1953 + 488 - 19 + 4 + 15 ) mod 7 ' = 2443 mod 7 ' = 0 ' El valor cero(0) corresponde al domingo. '--------------------------------------------------------------- '' ' cociente= Math.DivRem(dividendo, divisor, resto) ' Variable resto (valor de retorno) contiene el resto de la división, no se emplea ' Utilizo la función [Math.DivRem] porque a la hora de dividir daban ' problemas los redondeos y el resultado no resultaba correcto Dim resto As Integer = 0 ' no se emplea ' Dim a As Integer a = Math.DivRem((14 - mes), 12, resto) ' Dim a As Integer = ctype((14 - auxMes) / 12), integer) Dim y As Integer = año - a Dim m As Integer = mes + 12 * a - 2 Dim d As Integer = 0 '------------------------------------------------------------------------- ' auxDia + y + y / 4 - y / 100 + y / 400 + (31 * m) / 12) Mod 7) Dim y4 As Integer = Math.DivRem(y, 4, resto) Dim y100 As Integer = Math.DivRem(y, 100, resto) Dim y400 As Integer = Math.DivRem(y, 400, resto) Dim m12 As Integer = Math.DivRem((31 * m), 12, resto) ' d = dia + y + y4 - y100 + y400 + m12 d = d Mod 7 ' Return d End Function
El codigo de comprobacion de la funcion es el siguiente
Public Shared Function MiDayOfWeekTest() As String Using SW As New System.IO.StringWriter(System.Globalization.CultureInfo.CurrentCulture) SW.WriteLine("") SW.WriteLine(" ========================================================= ") SW.WriteLine("Prueba funcion [MiDayOfWeekTest] ") ' 2 August 1953 =0 SW.Write(MiDayOfWeekTestAux("1953-08-02", 0)) ' dia primero del año uno de enero ' que empieza el 1=lunes 2 = martes, etc SW.Write(MiDayOfWeekTestAux("2007-01-01", 1)) SW.Write(MiDayOfWeekTestAux("2008-01-01", 2)) SW.Write(MiDayOfWeekTestAux("2003-01-01", 3)) SW.Write(MiDayOfWeekTestAux("2009-01-01", 4)) SW.Write(MiDayOfWeekTestAux("2010-01-01", 5)) SW.Write(MiDayOfWeekTestAux("2005-01-01", 6)) SW.Write(MiDayOfWeekTestAux("2006-01-01", 0)) ' dia de fin de año 31 de diciembre del año ' que empieza el 1=lunes 2 = martes, etc SW.Write(MiDayOfWeekTestAux("2007-12-31", 1)) SW.Write(MiDayOfWeekTestAux("2002-12-31", 2)) SW.Write(MiDayOfWeekTestAux("2008-12-31", 3)) SW.Write(MiDayOfWeekTestAux("2009-12-31", 4)) SW.Write(MiDayOfWeekTestAux("2010-12-31", 5)) SW.Write(MiDayOfWeekTestAux("2005-12-31", 6)) SW.Write(MiDayOfWeekTestAux("2006-12-31", 0)) ' -------------------------- SW.WriteLine("Prueba TERMINADA ") SW.Flush() Return SW.ToString End Using End Function
y la funcion auxiliar que hace los calculos para cada fecha
Private Shared Function MiDayOfWeekTestAux( _ ByVal unaFecha As String, ByVal resultadoEsperado As Integer) As String Dim valorCalculado As Integer = 0 Dim salida As String = String.Empty Dim fechaTesteada As Date = Date.Parse(unaFecha) valorCalculado = DayOfWeekZeller(fechaTesteada) ' resultadoObtenido = FuncionesDeFechas.ISO8601ToDateWeek(fechaControl, True) If valorCalculado <> resultadoEsperado Then salida = String.Format("*** ERROR *** Fecha = {0} // Esperada = {1} // Obtenida = {2}", _ fechaTesteada.Date.ToShortDateString, resultadoEsperado, valorCalculado) & _ Environment.NewLine End If Return salida End Function