Introduction
Si nos preguntasen: "¿qué ha hecho la física cuántica por ti?", tal vez no sabríamos qué responder. Y sin embargo, nuestra vida cotidiana está plagada de aparatos y dispositivos cuyo funcionamiento se basa en las leyes de la mecánica cuántica: desde los transistores integrados a escalas masivas en los procesadores de nuestros ordenadores y teléfonos móviles, hasta los láseres que nos permiten escuchar CD musicales o ver películas en DVD, pasando por el receptor GPS para guiarnos por las carreteras o los relojes atómicos para conocer la hora con gran precisión.
A pesar de lo maravilloso de estos inventos, lo mejor está aún por llegar, de la mano de la revolución en la información cuántica. Los científicos están comenzando a explotar las paradójicas propiedades del mundo cuántico para construir nuevos sistemas de procesamiento y de transmisión de información. Una de tales paradojas es que enviar y almacenar información secreta será más fácil y difícil a la vez: por un lado, en el mundo cuántico pueden enviarse mensajes de manera totalmente segura, mientras que por otro lado pueden construirse ordenadores capaces de atacar los algoritmos de criptografía actuales.
Aunque todavía los ordenadores cuánticos quedan lejos en el horizonte, los primeros sistemas comerciales de criptografía cuántica ya están a la venta. En este artículo se arroja una mirada crítica a los logros actuales de la criptografía cuántica.
La criptografía cuántica no existe
La computación cuántica constituye un nuevo paradigma computacional basado en la mecánica cuántica, que encierra la promesa de resolver eficientemente problemas como la factorización de enteros, el logaritmo discreto y la simulación cuántica (véase el recuadro Computación cuántica). Los ordenadores cuánticos no manipularán bits de información, sino bits cuánticos o qubits, los cuales poseen la sorprendente propiedad de representar el estado "1" ó "0" simultáneamente.
A pesar de tratarse de uno de los campos de investigación más activos de la actualidad, lo cierto es que a día de hoy solamente existen algunos pequeños prototipos de procesadores de laboratorio capaces de manejar unos pocos qubits, pero nada que podamos llamar propiamente un ordenador cuántico, comparable a nuestros ordenadores.
Por usar un símil con la informática clásica, ni siquiera nos encontramos en la época pionera del ENIAC o del Colossus, primeros proto ordenadores concebidos durante la década de los 40 precisamente en el seno de la criptografía, equipados con válvulas de vacío, diodos de cristal y relés. La informática y con ella la revolución de las comunicaciones no despegó hasta la invención del transistor por los Laboratorios Bell en 1947. El transistor dio lugar a los circuitos integrados y demás elementos de la alta escala de integración y posibilitó la construcción de ordenadores cada vez más pequeños, según la famosa Ley de Moore, propuesta en 1965 por Gordon Moore, cofundador de lntel. Ahora bien, cuando la miniaturización alcanza la escala atómica, o se busca un nuevo paradigma computacional o no es posible seguir miniaturizando. Hoy por hoy, no se ha descubierto el elemento cuántico que permita la alta integración y escalabilidad, posibilitando así el despegue de la computación cuántica.
Para crear un ordenador cuántico se necesita un sistema físico que se comporte cuánticamente durante un período de tiempo suficientemente largo y que pueda ser accedido y manipulado fácilmente. Se está experimentando intensamente en laboratorios de investigación de todo el mundo con qubits basados en partículas cuánticas (átomos, fotones, etc.) o qubits basados en estructuras macroscópicas a las que se obliga a comportarse cuánticamente. Algunos laboratorios han conseguido crear métodos de control cuánticos que manejan hasta 12 qubits, mientras que sólo se han conseguido procesadores cuánticos de 2 qubits que realicen un algoritmo. Además, todos requieren una complicada y costosa tecnología, generan tasas de errores de hasta el 20 por ciento y sus qubits poseen tiempos de vida de menos de 1 microsegundo. Para poder ser práctica, la computación cuántica necesitaría miles de qubits, hoy por hoy nada más que un sueño de ciencia ficción.
Por otro lado, aunque se han ideado numerosos algoritmos cuánticos para efectuar tareas como factorizar enteros o realizar búsquedas en una base de datos, no existe propiamente ningún algoritmo cuántico de criptografía.
Por lo tanto, si aún no existen los ordenadores cuánticos ni existen algoritmos cuánticos de criptografía, ¿podemos hablar de criptografía cuántica? Con propiedad, no. Hoy en día, lo que todo el mundo entiende cuando se menciona el término criptografía cuántica es en realidad la distribución cuántica de claves.
El problema de la distribución de claves
A día de hoy la distribución cuántica de claves constituye un caro capricho tecnológico para organizaciones con elevados recursos y grandes requisitos de seguridad
Durante siglos el hombre se ha esforzado por proteger la información. Así fue como nació y fue evolucionando la criptografía, con sus distintos algoritmos de cifrado. Sin embargo, un problema que trajo de cabeza a criptógrafos de todas las épocas fue el de la transmisión de claves. Por muy perfecto y seguro que sea un algoritmo de cifrado, necesita utilizar una clave para cifrar y descifrar. ¿Cómo hacer para transmitir la clave de manera segura? De nada sirve proteger criptográficamente los mensajes si un intruso puede robar con facilidad la clave usada para cifrarlos. Históricamente se usaron todo tipo de soluciones parciales e insatisfactorias al problema de distribución de claves: desde palomas a mensajeros custodiados por soldados. Desgraciadamente, o no alcanzaban una seguridad razonable, o resultaban logísticamente inviables para escenarios con multitud de usuarios. Después de la Segunda Guerra Mundial, a medida que la criptografía se popularizó fuera de círculos militares y diplomáticos, la distribución de claves parecía un problema insoluble: si dos partes deseaban comunicarse mediante mensajes cifrados, necesitaban confiar en una tercera parte para transmitir las claves de cifrado, la cual pasaba a convertirse en el eslabón más débil de la cadena de seguridad. La criptografía parecía haber llegado a un punto muerto, un callejón sin salida que la ponía fuera del alcance de civiles y pequeñas empresas.
No fue hasta el año 1976, cuando Whitfield Diffie y Martin Hellman inventaron la criptografía de clave pública, que pudo atisbarse la luz al final del túnel. Tras la propuesta del algoritmo RSA por Rivest, Shamir y Adleman pudieron por primera vez en la Historia transmitirse de manera razonablemente segura claves de cifrado entre varias partes sin necesidad de que éstas se conocieran previamente ni de utilizar mensajeros de confianza. Se había resuelto el problema de la distribución de claves. La criptografía se democratizó, quedando por fin al alcance de todas las personas.
A pesar de las innegables virtudes de los algoritmos de clave pública como RSA, lo cierto es que se basan en la premisa nunca demostrada de que no es posible resolver en tiempo polinómico ciertos problemas difíciles de matemáticas, como por ejemplo, la factorización de números enteros compuestos por el producto de dos primos. En otras palabras, nadie sabe si RSA y otros algoritmos parecidos son de verdad seguros.
Y lo que es peor, como se explica en el recuadro ¿Sueñan los crackers con ordenadores cuánticos?, los ordenadores cuánticos podrían imp1ementar algoritmos capaces de factorizar números enteros grandes, como los utilizados en las claves RSA, lo que significaría el fin de la criptografía de clave pública tal y como la conocemos. En este panorama tan poco halagüeño, la distribución cuántica de claves ofrece la promesa de distribuidas de manera cien por cien segura. ¿Cómo es esto posible?
Qué es y para qué sirve la distribución cuántica de claves
La piedra angular de la criptografía cuántica es el principio de incertidumbre de Heisenberg que, como aprendimos en la Universidad, nos enseña que no pueden conocerse simultáneamente con exactitud dos variables complementarias, como la posición y la velocidad, de una partícula. Supongamos entonces que tenemos un fotón que puede estar polarizado en una de cuatro direcciones distintas: vertical (|), horizontal (-), diagonal a la izquierda (\) o diagonal a la derecha (/). Estas cuatro polarizaciones forman dos bases ortogonales: por un lado, I y -, a la que llamaremos base (+), y por otro lado, /y \, a la que llamaremos (x).
Pues bien, el principio de incertidumbre de Heisenberg, por irracional que nos parezca, impide que podamos saber en cuál de las cuatro posibles polarizaciones se encuentra el fotón. Para conocerla, deberíamos utilizar un filtro, que podríamos imaginamos como una ranura en una lámina, que tuviera la orientación, por ejemplo, vertical (|). Es evidente que los fotones con la misma polarización pasarán, mientras que los polarizados horizontalmente, y por lo tanto, perpendiculares al filtro, no pasarán. Sorprendentemente, ¡la mitad de los polarizados diagonalmente pasarán y serán reorientados verticalmente! Por lo tanto, si se envía un fotón y pasa a través del filtro, no puede saberse a ciencia cierta si poseía polarización vertical o diagonal, tanto \ como /. Igualmente, si no pasa, no puede afirmarse que estuviera polarizado horizontal o diagonalmente. En ambos casos, un fotón con polarización diagonal podría pasar o no con igual probabilidad.
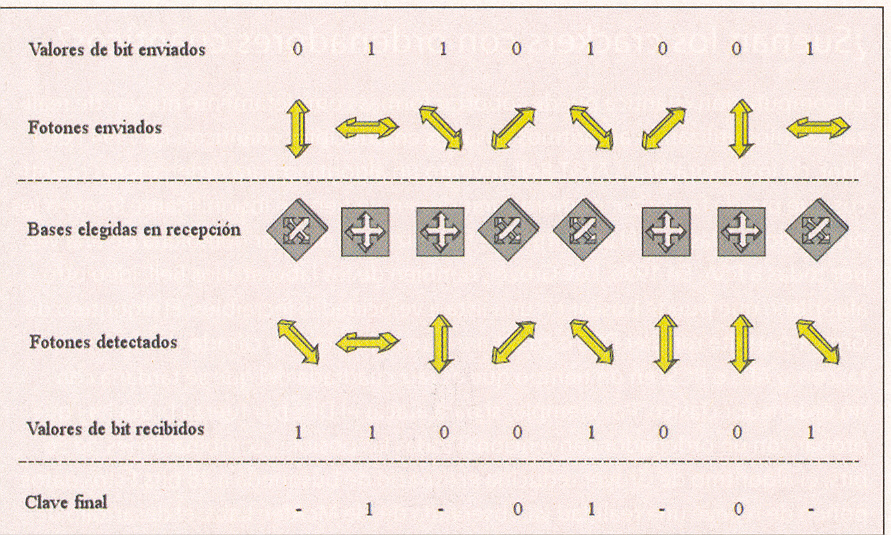
Para utilizar estos increíbles resultados en distribución de claves, se acuerda representar un 1 o un 0 de información según la polarización de los fotones que se envían. Así, en la base rectangular (+), un 1 vendría representado por una polarización |, mientras que un 0, por - mientras que en la base diagonal (x), el 1 sería la polarización / y el 0, \. En estas condiciones, para enviar un mensaje binario, Alicia va enviando fotones a Bernardo con la polarización adecuada, cambiando aleatoriamente de una base a otra.
Si un intruso, Ignacio, intercepta los fotones y mide su polarización utilizando un filtro, digamos (|), debido al principio de incertidumbre nunca podrá saber si los fotones pertenecían a la base + o x. Por lo tanto, nunca sabrá qué mensaje se envió, da igual qué tipo de filtro utilice. Ahora bien, algún lector ya se estará dando cuenta de que si Ignacio se encuentra con este dilema, lo mismo le ocurrirá a Bernardo.
Efectivamente, emisor y receptor no pueden acordar de antemano qué bases se utilizarán para enviar cada fotón, porque entonces nos encontraríamos con el problema de cómo hacerse llegar mutuamente de forma segura esa lista de bases y volveríamos al principio. En 1984 Charles Bennet y Gilles Brassard idearon el siguiente método para hacer llegar el mensaje al destinatario sin necesidad de recurrir a otros canales de distribución. En primer lugar, debe allanarse el camino mediante los siguientes tres pasos:
- Paso 1: Alicia le envía a Bernardo una secuencia aleatoria de 1's y 0's, utilizando una elección aleatoria entre las bases + y x.
- Paso 2: Bernardo tiene que medir la polarización de estos fotones. Para ello, utiliza aleatoriamente las bases + y x. Claro está, como no tiene ni idea de qué bases utilizó Alicia, la mitad de las veces estará eligiendo mal la base.
- Paso 3: para resolver esta situación, Alicia llama a Bernardo por teléfono, o se conectan a un chat, o utilizan cualquier otro canal de comunicaciones inseguro, sin preocupar1es si son espiados por Ignacio, y le cuenta qué base de polarización utilizó para cada fotón que envió, + o x, aunque no le dice qué polarización concreta. En respuesta, Bernardo le cuenta a Alicia en qué casos ha acertado con la polarización correcta y por lo tanto recibió el 1 ó 0 sin error. Ahora ya, ambos eliminan los bits que Bernardo recibió con las bases erróneas, quedando una secuencia un 50 por ciento menor que la original, que constituye la clave de una cinta aleatoria cien por cien segura, puesto que se generó de forma completamente aleatoria por ser derivada de una secuencia original de 1's y 0's aleatoria.
¿Y qué ocurre con el malvado Ignacio? Para su desgracia, aunque intercepte los mensajes de Alicia y Bernardo, sólo obtendría un 25 por ciento de la secuencia inicial y el 50 por ciento de la secuencia una vez corregidas las bases. Más aún, la mera presencia de Ignacio en la línea será detectada, ya que si mide la polarización de un fotón con el detector equivocado, la alterará. Lamentablemente, como el lector avispado se dará cuenta, esta alteración impediría que Alicia y Bernardo pudieran ponerse de acuerdo acerca de la secuencia aleatoria a usar como cinta, debido a que, si Ignacio cambió la polarización de un fotón por el camino, podrían obtener distintos bits incluso aunque utilicen las mismas bases.
Por consiguiente, hace falta un método para detectar que Ignacio no esté haciendo de las suyas. En realidad, resulta tan sencillo como sigue: Bernardo le cuenta a Alicia, utilizando el mismo u otro canal inseguro, cuáles son los primeros, digamos que, 50 bits de su clave aleatoria. Si coinciden con los de Alicia, entonces saben que Ignacio no les espió ni el canal tiene ruido y utilizan con seguridad el resto de los bits generados. Si no coinciden, ya saben que Ignacio metió la manaza por medio o utilizaron un canal muy ruidoso y por lo tanto deben desechar la clave entera.
En 15 años, puede decirse que no se han producido muchos más avances teóricos en el campo de la (mal llamada) criptografía cuántica, aunque se han dado pasos de gigante en cuanto a la implementación tecnológica de lo que, de otra forma, habrían terminado como elucubraciones mentales para juegos de salón. Manipular fotones individuales constituye todo un desafío de ingeniería, que fue aceptado con entusiasmo por Bennet y un estudiante. Y así, en 1989, consiguieron la primera transmisión de señales cuánticas de la historia a una distancia de 32 cm. ¡El sueño de la distribución cuántica de claves (QKD) por fin se hacía realidad!
Avances en distribución cuántica de claves
Desde la primera vez que fue demostrada experimentalmente, los avances en los sistemas de distribución cuántica de claves han sido continuos. El canal de transmisión de los estados cuánticos que cifran la clave en estos sistemas suele ser la clásica fibra óptica o el espacio libre, ya que la atmósfera es un buen transmisor de las longitudes de onda típicas de estos sistemas. Los sistemas que utilizan fibra han avanzado considerablemente, especialmente en minimizar los efectos de degradación que sufren los delicados estados cuánticos al ser transmitidos por un medio que, al fin y al cabo, no es ideal. Por ello se han diseñado sistemas inteligentemente auto compensados que transmiten eficientemente los estados cuánticos eliminando los efectos negativos que introduce la fibra óptica.
Los sistemas en espacio libre también han avanzado considerablemente desde aquella primera transmisión a sólo 32 cm de distancia a finales de los 80. Los sistemas actuales son capaces de transmitir a más de 100 Km claves cuánticas y cuentan con complejos sistemas de seguimiento y alineación
El primer sistema que utilizó fibra están dar de telecomunicaciones para transmitir claves cuánticas nació en 1993 de una colaboración entre British Telecom y una compañía británica de defensa QinetiQ. Lograron una transmisión en laboratorio utilizando un rollo de fibra estándar de 10 Km de longitud. Dos años después consiguieron aumentar la distancia a 30 Km al mismo tiempo que investigadores de la Universidad de Ginebra consiguieron alcanzar los 23 Km, pero utilizando fibra óptica instalada por una compañía de telecomunicaciones y con un sistema mucho más estable. En 2002 la distancia se aumentó hasta los 67 Km por este mismo grupo y nació el primer producto comercial de transmisión cuántica de claves. Actualmente, el récord de distancia de transmisión lo ostenta el laboratorio de Los Álamos y el NIST con 150 Km de transmisión cuántica obtenida.
Por su parte, en enlaces aéreos la distancia más larga ha sido de 16 Km, en una colaboración de lo más selecto de la investigación europea en este campo en el que se lograron mandar claves cuánticas desde la isla de la Palma a Tenerife y cuyos resultados fueron publicados en la revista Nature. Los enlaces aéreos despiertan un interés especial ya que en un principio podrían suponer la comunicación segura a nivel global.
La transmisión en fibra óptica presenta un serio inconveniente, ya que la distancia máxima está limitada por las pérdidas en la fibra. A diferencia de un sistema convencional, los sistemas cuánticos no permiten la utilización de amplificadores ópticos, los cuales recuperan la señal cuando ésta pierde intensidad, ya que estos perturbarían los estados cuánticos de la clave. Sin embargo, un enlace aéreo entre dos puntos que incluyera un satélite en baja órbita terrestre como intermediario resolvería este problema, ya que el emisor podría mandar la clave al satélite, que a su vez la transportaría al lugar deseado para posteriormente reenviársela al receptor. Sin embargo una transmisión real por satélite está todavía lejos de realizarse, si bien los retos tecnológicos que se presentan no son insalvables.
¿A quién beneficia la distribución cuántica de claves?
Hoy por hoy, la distribución cuántica de claves es una tecnología inmadura con una serie de importantes limitaciones:
Sólo sirve para crear enlaces punto a punto utilizando redes pasivas, bien por fibra óptica, bien por enlace aéreo, como por ejemplo dos sucursales bancarias en la misma ciudad. No es posible que dos usuarios puedan enviarse claves si no han creado previamente este enlace. El equipamiento para crear estos enlaces es muy caro
La velocidad de transmisión de claves es todavía muy lenta. Las soluciones comerciales ofrecen velocidades del orden de 1 Kbps Para hacemos una idea de la magnitud de esta velocidad, para transmitir un DVD se tardaría más de un año. Resultaría más rápido enviar la clave con un mensajero.
Las distancias de conexión son todavía muy cortas, de hasta 150 Km.
El problema de la autenticación está aún sin resolver de manera satisfactoria. ¿Cómo sabe Alicia quién está al otro lado de la comunicación? Las soluciones propuestas hasta la fecha se basan en compartir previamente una clave antes de empezar la distribución de claves, pero nos retrotrae al problema original: ¿cómo comparto esa clave inicial de manera segura?
Por consiguiente, podemos afirmar que a día de hoy la distribución cuántica de claves constituye un caro capricho tecnológico para organizaciones con elevados recursos y grandes requisitos de seguridad, como por ejemplo los bancos o los militares, que necesitan transmitir claves de forma segura entre unos pocos puntos clave. El resto nos seguiremos conformando de momento y por mucho tiempo con la criptografía de clave pública y los certificados digitales. pcw
Más información
Tanto los ordenadores clásicos como los hipotéticos ordenadores cuánticos realizan cálculos mediante la manipulación de unidades de información. Los ordenadores clásicos representan la información como dígitos binarios o bits, los cuales pueden tomar uno de dos posibles valores "0" o "1". Os ordenadores cuánticos representa la información como bits cuánticos o qubits. Se pueden utilizar muchos objetos físicos como qubits: por ejemplo átomos, fotones o electrones. Paradójicamente, un qubit puede representar simultáneamente el valor "0" o "1", así como cualquier ore valor intermedio, gracias a la propiedad de superposición de estados cuánticos. De esta forma, un ordenador cuántico puede realizar en paralelo operaciones sobre los qubits de entrada calculando todos los posibles valores de salida a la vez en lugar de tener que hacerlo secuencialmente de uno en uno como en computación clásica. Esta posibilidad de paralelización hace que algunos algoritmos cuánticos sean tan eficientes al realizar tareas clásicas
La computación cuántica puede soportar formas completamente nuevas de realizar cálculos utilizando algoritmos basados en principios cuánticos. En 1994 Peter Shor, de los laboratorios At&T Bell, invento un algoritmo para ordenadores cuánticos que puede factorizar números grandes en un tempo insignificante frente a los ordenadores clásicos. El algoritmo de factorización de Shor demolería de una vez por todas a RSA. En 1996, Low Grover, también de los laboratorios Bell, ideo otro algoritmo que puede buscar en una lista a velocidades increíbles. El algoritmo de Grover permite romper DES o cualquier otro algoritmo de cifrado de clave secreta como AES o RC5, en un tiempo que es raíz cuadrada del que se tardaría con un ordenador clásico. Por ejemplo, si para atacar DES por fuerza bruta hay que probar con un ordenador convencional todas las combinaciones posibles de 56 bits, el algoritmo de Grover reduciría el espacio de búsqueda a 28 bits. Estos datos ponen de relieve una realidad ya observada desde McAfee Labs: el desarrollo de programas nocivos se centra en entornos multiplataforma.
Referencia Bibliográfica
Verónica Fernández Mármol y Gonzalo Álvarez Marañón trabajan en el Grupo de Investigación en Criptología y Seguridad de la Información del CSIC.
Artículo completo publicado en la revista WWW.PCWORLD.ES FEBRERO 2010